Research Highlights
For further details, see my list of my publications.
Editing and attacking large language models
What if a piece of malware could secretly attack your language model’s weights?
What if this caused the model to produce an attacker’s chosen response to their chosen prompt?
What if seemingly all current families of large language models were susceptible to such attacks?
Would you still trust the model to run code on your computer or access databases?
These are exactly the questions we ask in our recent preprint. We investigate the problem of editing language models, i.e. directly tweaking their weights in such a way that they produce a chosen response to a specific prompt, without otherwise affecting their behaviour. The appeal of being able to do this is that such surgical interventions into a model can be used to correct hallucinations as they are found, without the expense of fine-tuning the model, or the risk of accidentally introducing unknown new problems. However, flexible models which can be easily edited carry the risk of what we call stealth attacks: small, difficult to detect edits made to a model by an adversary.
By exposing the theoretical foundations of model editing, we are able to directly predict how easily a given model can be successfully edited using a simple metric. This metric measures a specific notion of the intrinsic dimension of the model’s latent features, a measure we previously introduced when studying classification problems. We use this to design a new editing method, which optimises our intrinsic dimensionality metric, operates analogously to existing methods such as GRACE and Transformer-Patcher, and uses only standard neural network operations. The editing method is simple enough that it can be run on a laptop in many cases, and could even be implemented in malware. In the process, we reveal that the probability of successful editing with methods such as GRACE and Transformer-Patcher is also controlled directly by our metric.
Open source implementations of our algorithms are available, and we have a demo where you can try it out for yourself!
For full details and plenty of experiments, see our preprint:
O. J. Sutton, Q. Zhou, W. Wang, D. J. Higham, A. N. Gorban, A. Bastounis, I. Y. Tyukin (2024). Stealth edits for provably fixing or attacking large language models, arXiv, 2406.1267.
For further details about the intrinsic dimensionality metric, see our earlier work:
O. J. Sutton, Q. Zhou, A. N. Gorban, I. Y. Tyukin (2023). Relative intrinsic dimensionality is intrinsic to learning, International Conference on Artificial Neural Networks (ICANN) 2023, vol 14254, pp 516-529, Springer, Cham..
Can random noise certify robustness against adversarial attacks?
According to our recent reseach, the answer is no!
Adversarial attacks exploit hidden sensitivities in modern neural networks. A piece of input data, which would ordinarily be classified accurately, is slightly modified in a way which makes the classifier produce wildly incorrect predictions – even when the modification is so small that it is imperceptible to a human. Hidden instabilities such as these are clearly dangerous in the real world, where incorrect decisions can have dire consequences.
Much research has therefore been put into both defending networks against adversarial attacks and devising systems for certifying that they are not susceptible to them. The modifications applied to create adversarial attacks are so small that it is tempting to think that if you can certify that large quantities of big, randomly generated perturbations are very unlikely disrupt the classifier, then small adversarial perturbations shouldn’t either.
Unfortunately this thinking turns out to be a false: robustness to random perturbations provides no indication of robustness to adversarial perturbations! We prove this mathematically in the article for for various realistic model classifiers, and demonstrate it empirically for the CIFAR-10 dataset (see the example figures). We prove that classifiers dealing with high dimensional data can simultaneously have the following features: high accuracy on unseen testing data, high probability of stability to randomly sampled perturbations, yet vulnerability to easily computable destabilising adversarial perturbations.
These results draw a sharp distinction between the concepts of probabilistic stability (the model is insensitive to large random perturbations with high probability) and deterministic instability (there exists a small adversarial attack affecting the model). Certifying that a given model provides one is no guarantee of the other!
Complete details of these results are available in the preprint of our article:
O. J. Sutton, Q. Zhou, I. Y. Tyukin, A. N. Gorban, A. Bastounis, D. J. Higham (2023). How adversarial attacks can disrupt seemingly stable accurate classifiers, arXiv, 2309.03665.




The inevitability, typicality and undetectability of instability in neural networks
How stable are classifiers built around neural networks? This is a key question being widely asked with the rush to prominence of neural network-based AI tools.
In a recent article, presented at ICANN 2023, we provide a mathematical answer. Not only is instability (high sensitivity to small perturbations of the input data) to be expected in neural networks, but it can also be remarkably widespread, yet can only be detected by sampling vast quantities of training and test data. More specifically, we show that there exist uncountably large families of binary classification problems where standard neural network training techniques will produce an accurate network which contains hidden sensitivities. Although the network successfully classifies all training, validation and testing data, it is susceptible to miniscule modifications to pieces of data (e.g. adversarial attacks), leading to misclassifications.
Despite this, we show that there exists a stable neural network – with the same architecture as the unstable network! This stable network even minimises the same loss function, and can have all its weights arbitrarily close to those of the unstable network. Standard techniques such as weight regularisation, however, will push towards the unstable solution.
Astonishingly, this problem is already present in standard feed-forward neural networks with input dimension dimension n which have just order n neurons arranged in two layers. Larger neural networks can be similarly affected simply because they contain such a sub-network.
All this is discussed in detail, along with some other surprising features of neural networks, in our recent paper:
A. Bastounis, A. N. Gorban, A. C. Hansen, D. J. Higham, D. Prokhorov, O. J. Sutton, I. Y. Tyukin and Q. Zhou (2023). The boundaries of verifiable accuracy, robustness, and generalisation in deep learning, International Conference on Artificial Neural Networks (ICANN) 2023, vol 14254, pp 530-541, Springer, Cham..
When can machines learn from just a few examples?
Machine Learning and Artificial Intelligence have seemingly become synonymous with Big Data – we imagine neural networks and other tools being trained on vast datasets to learn to perform tasks. But is it possible for these systems to learn from small datasets consisting of just a few (e.g. 5 or 10) examples of a new class of objects?
In a recently submitted article we investigate just this question. We build on existing work showing that implicit properties of high dimensional spaces can make learning from few examples possible in certain circumstances using very simple linear classifiers (a so-called blessing of dimensionality). We are particularly interested in whether nonlinear feature maps, i.e. nonlinear mappings of the dataset into much higher dimensional spaces, can accelerate the onset of this blessing of dimensionality, thereby enabling algorithms to learn from few examples. We are able to provide specific relationships between the distributions of the data classes we are learning, the geometry of the feature mappings, and the probability of successfully learning from just a few examples. To illustrate our results, we consider the MNIST handwritten digit recognition problem. We first train a (relatively simple) neural network to recognise 9 of the 10 digits. We then build a simple Fisher linear discriminant classifier in feature space to recognise the remaining (previously unseen) digit using just 10 training examples. Surprisingly, the AI is able to successfully recognise the extra digit, even though it never saw it while the underlying network was being trained and only saw a few examples of it during calibration!
To find out more about how this works and when it is possible, see our arXiv preprint:
O. J. Sutton, A. N. Gorban and I. Y. Tyukin (2022). Towards a mathematical understanding of learning from few examples with nonlinear feature maps, arXiv, 2211.03607.
Part of this work was also published at the London Computing Conference 2023 (where it won the best paper award):
I. Y. Tyukin, O. J. Sutton, A. N. Gorban (2023). Learning from few examples with nonlinear feature maps, Science and Information Conference (2023), vol 711, pp 210-225, Springer, Cham..
and at Geometric Science of Information 2023:
O. J. Sutton, A. N. Gorban and I. Y. Tyukin (2023). A geometric view on the role of nonlinear feature maps in few-shot learning, Geometric Science of Information (GSI) 2023, vol 14071, pp 560-568, Springer, Cham..
New efficient algorithms for simulating the propagation of radiation
Simulating how radiation (for example gamma rays) propagates through a medium is a fundamental problem in many fields of applied science. This includes fields such as designing nuclear reactors, optimising radiation beams for radiotherapy, and reconstructing images in CT scanners. As might be expected, this is a field with a long history and many important contributions dating back to the work of Chandrasekhar in the 1920s.
Recently, we were able to present a new family of highly efficient numerical methods for solving this class of problems. From a mathematical modelling perspective, the physical process of radiation transport is governed by the Boltzmann transport equation, a partial integro-differential equation posed in six independent variables - three spatial variables, two angular directional variables and one energy variable.
Our new algorithms can be implemented in exactly the same efficient form as existing standard multigroup discrete ordinates methods - meaning that an implementation only has to solve a collection of linear transport problems in the spatial variables and can do so in parallel. However, optimised design choices mean that the methods can be proven to converge at arbitrarily high order under suitable assumptions on the problem data, and are ideally suited to hp-adaptive meshing. The mathematical convergence results we present are also the first for radiation transfer problems, and explicitly take into account the discretisations used in space, angle and energy.
Full details of the algorithm, its stability and error analysis, and its efficient implementation are given in our recent article:
P. Houston, M. E. Hubbard, T. J. Radley, O. J. Sutton and R. S. J. Widdowson (2024). Efficient high-order space-angle-energy polytopic discontinuous Galerkin finite element methods for linear Boltzmann transport, Journal of Scientific Computing, vol 100 (52).
Adaptive polygonal meshes for parabolic problems, using virtual element methods
We have extended our previous work (described below) on numerical methods using adaptive polygonal meshes to (time dependent) parabolic problems. This means that aggressive mesh coarsening becomes a real possibility, since patches of elements with low error can simply be merged together. In particular, this allows the shape of the mesh to directly match the shape of the solution being approximated, as shown in the videos here. The key to the argument turned out to be in deriving new error estimators which were applicable even when the finite element spaces may be completely different between time-steps - i.e. they are non-hierarchical. Our estimates are therefore also applicable to moving mesh methods and other schemes presenting similar non-hierarchicalities.
The full details of this research can be found in our article:
A. Cangiani, E. H. Georgoulis, and O. J. Sutton (2021). Adaptive non-hierarchical Galerkin methods for parabolic problems with application to moving mesh and virtual element methods, Mathematical Models and Methods in Applied Sciences, 31 (4) 711-751.
To ensure that the estimator effectivities remain bounded with respect to time, the analysis adopts the time accumulation framework developed in my earlier paper:
O. J. Sutton (2020). Long-time L∞(L2) a posteriori error estimates for fully discrete parabolic problems, IMA Journal of Numerical Analysis, Volume 40, Issue 1, 498-529.
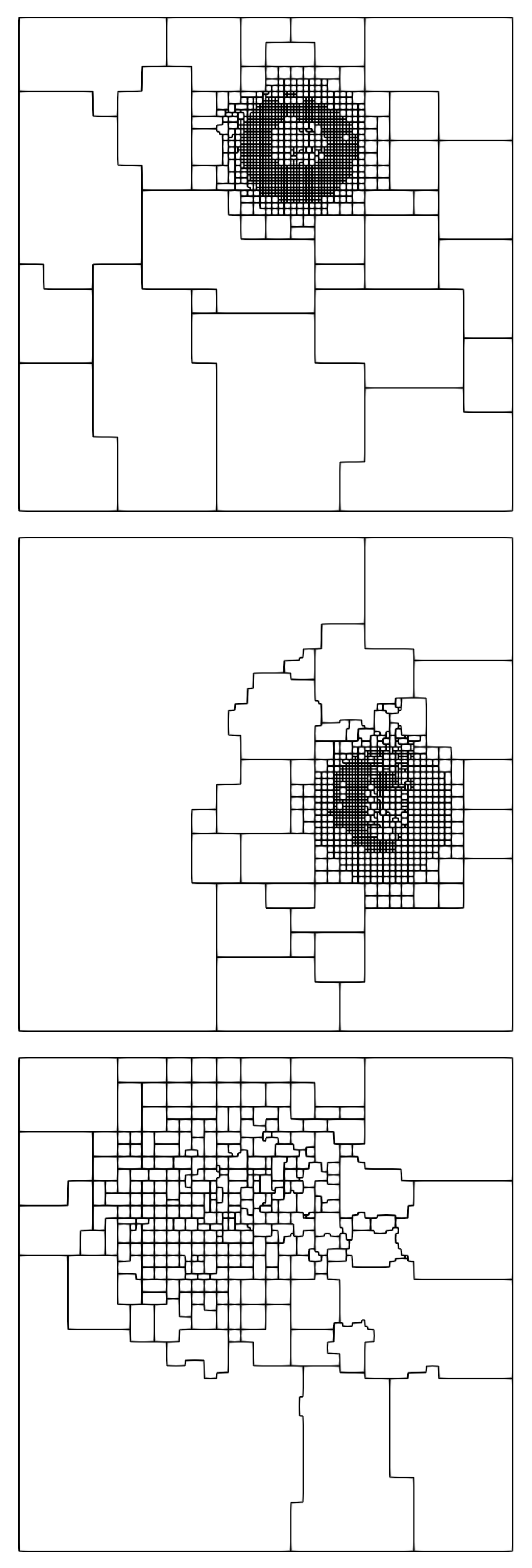
New pattern forming mechanisms in reaction-diffusion systems, discovered using an efficient computational framework
By developing an efficient computational framework, we have recently discovered entirely new pattern forming mechanisms in a time dependent reaction-diffusion system with a cyclic competition structure. Such systems describe a wide variety of natural phenomena, particularly the competion between certain groups of organisms. These interactions are structured like a game of rock-paper-scissors: species A outcompetes species B, species B outcompetes species C, and species C in turn outcompetes species A.
Some examples of these new patterns are shown here, with a different colour indicating the regions dominated by each of the three species. The patterns typically feature zones of chaos and zones of stable travelling structures. To produce these simulations, we developed an efficient computational framework based around an automatic adaptive algorithm for the computational mesh driven by rigorous new a posteriori estimates of the numerical simulation error.
A snapshot of these patterns was featured on the front cover of the May 2018 issue of Proceedings of the Royal Society A. For the full details of the patterns and the framework we developed to simulate them, see our paper:
A. Cangiani, E. H. Georgoulis, A. Yu. Morozov, and O. J. Sutton (2018). Revealing new dynamical patterns in a reaction-diffusion model with cyclic competition via a novel computational framework, Proceedings of the Royal Society A, 474 20170608.

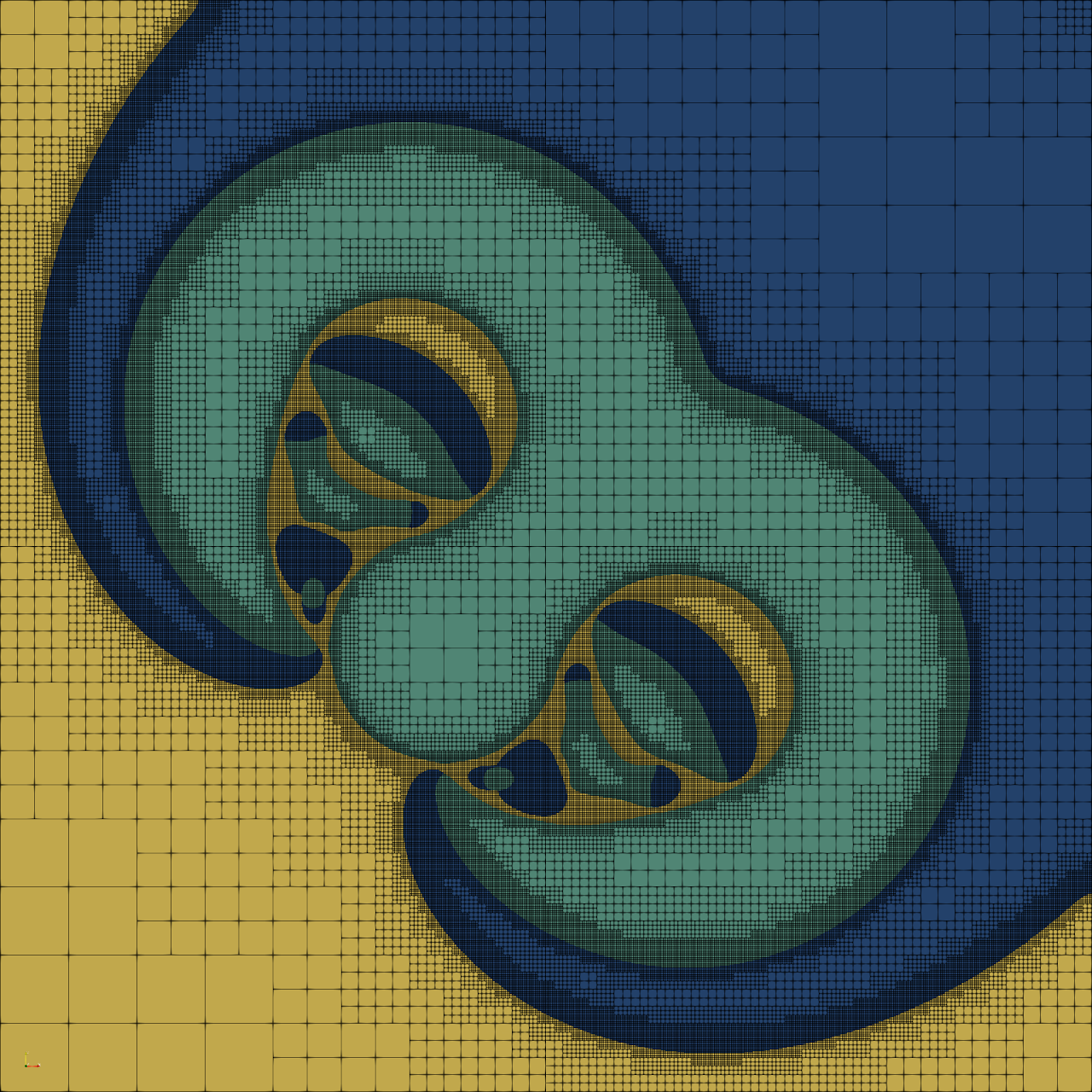
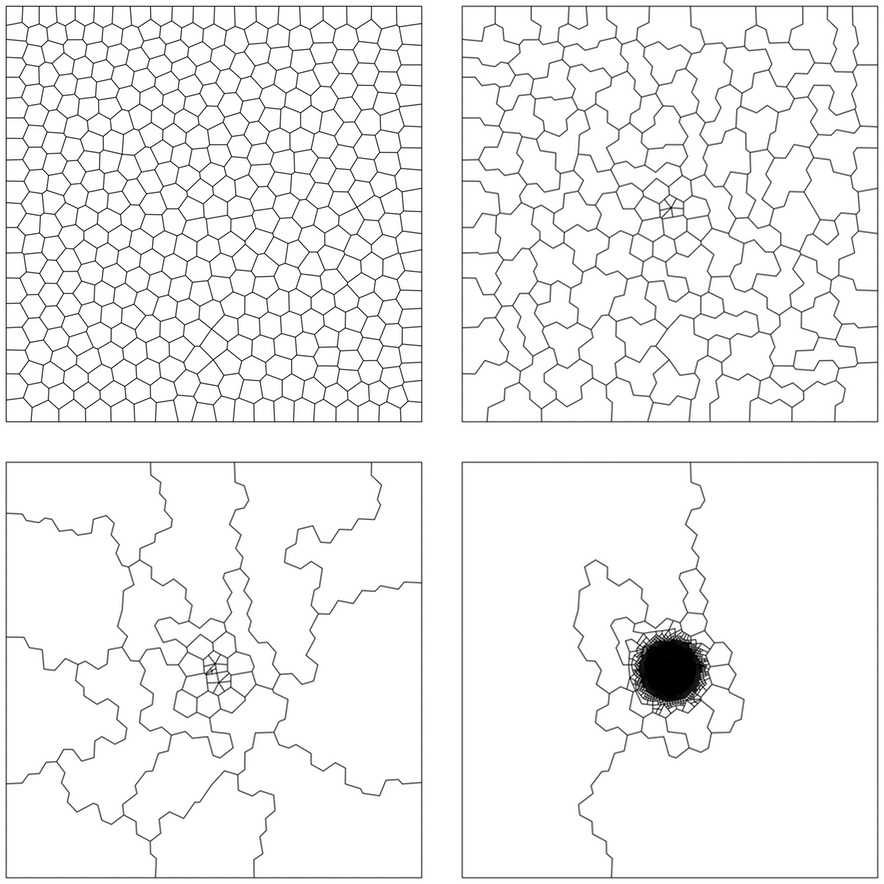
Solving elliptic problems using adaptive polygonal meshes, with virtual element methods
Numerical methods which use polygonal meshes bring with them the exciting prospect of very general adaptive meshing, allowing computational effort to be tightly focussed on areas of the domain where it is required. For instance, coarsening areas of the mesh becomes as simple as merging patches of elements, as demonstrated by the sequence of adapted meshes shown here.
This is something we have been recently exploring for elliptic problems by developing rigorous and computable local error estimators for virtual element methods. The full details can be found in our article:
A. Cangiani, E. H. Georgoulis, T. Pryer, and O. J. Sutton (2017). A posteriori error estimates for the virtual element method, Numerische Mathematik, 137(4), 857-893.
The analysis is based on the numerical scheme we developed in the article:
A. Cangiani, G. Manzini, and O. J. Sutton (2017). Conforming and nonconforming virtual element methods for elliptic problems, IMA Journal of Numerical Analysis, 37(3), 1317-1354.
The virtual element method: now in just 50 lines of Matlab!
The virtual element method is a recently introduced method for approximating solutions to partial differential equations using general polygonal meshes. To help clarify the design and implementation of the method, and show how the theory translates into practice, I have developed and dissected an accessible 50 line Matlab implementation for solving Poisson’s problem.
The code itself is available online, and has been downloaded over 700 times (it is also available through Netlib as the package na45 in the numeralgo library). The details of the formulation of the virtual element method for this problem, and a discussion of how each component may be implemented, is given in my article:
O. J. Sutton (2017). The virtual element method in 50 lines of MATLAB, Numerical Algorithms, 75(4), 1141-1159.